Professional Development
Implementing Research-Based Instruction in Introductory Proofs Courses
2025 MAA OPEN Math Workshop
June 9, 10, 12, & 13, 11am-5pm ET
Google Group: 2025-open-math-wksp-5@maa.org
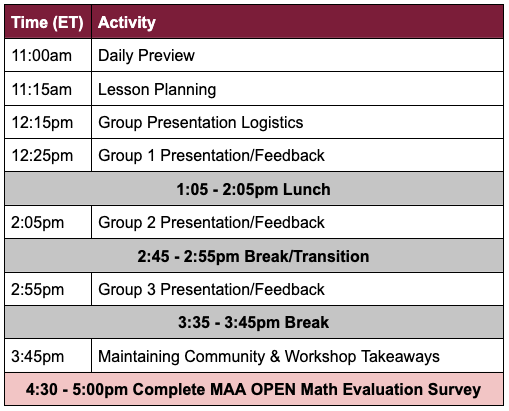
Please scroll below to see the schedule of activities followed by resources for each morning or afternoon activity.
In this activity you will:
- Solve a task.
- Watch a video of a student solving the task.
- Discuss the student's reasoning.
1. Solve the following task:
Decide whether the proof below does or does not prove the given claim. Explain your reasoning.

2. Watch this video of Mary's reasoning about the task:
Mary (00:00): I would say that that up till the part where they say that the statement is true, it works. Um Thus the negation statement to be proved is false. And hence the statement is true. I think that line doesn't work, but the rest of it does work because it's saying, okay, well let's say that it was true and let's try to prove it false and we'll use the bounds that we're given. And we're like, okay, so we're saying that it's true and we're going to try to see if it's false. And so we're just going to pick any two numbers, one and one. And so one plus one is two, square is four, and one squared plus one squared is two, which is not equal to four. So that proves that it's false, that any for any x for x is greater than zero and x and y is greater than zero, this equation does not hold true. So that means this is true. So I don't think their reasoning proves that this is a true statement, but they end with the statement, oh wait, nevermind. That's good. I just can't understand read words
Andy (01:19): Sometimes. So what, was there a strategy that made the, can you kind of read what their strategy was in this proof?
Mary (01:24): Yeah. So they were like, okay, well what if it is true? In this case we're saying that it's
Andy (01:29): The equation is true, you mean? Like the inequality?
Mary (01:30): What if the equation, the inequality, is true and it's not. And x plus y bracket squared is equal to x squared plus y squared. Then let's prove that. Let's have, let's set x equal to one and y equal to one, and just show that the two sides are equal to each other. But then you come out to see that the two sides are not equal to each other. So therefore this statement where it's equal to each other can't be true. And this statement is true because it is the opposite of that.
Andy (02:04): Okay
3. Discuss with your group: What do you notice about Mary’s thinking? In particular, what is she doing with quantification?
Consider the following conjecture: The sum of two odd integers is even.
Discuss with your group: When and how would you implement this conjecture as a task in class? (Consider opportunities for student contributions, lecture notes presented on board, etc.)
Discuss the following with your group:
- What do your students expect from you based on their school experience?
- What norms do you intend to establish?
- How are these norms enacted in your classroom?
- What are the challenges that you experience when trying to enact norms?

If you'd like to read more, browse The Proofs Project's Classroom Norms Module and/or check out the research article by Yackel & Cobb (1996) linked below.
In this activity you will:
- Solve a task.
- Watch a video of a student solving this task.
- Discuss with your group what you notice about the student's reasoning.
1. Solve the following task:
Let P and Q be events that have some nonzero probability of occurring, and suppose that the following two implications are true:
- If P and Q are mutually exclusive, their probabilities are not independent.
- If the probabilities of P and Q are independent, the probability of the product of P and Q is the probability of P and the probability of Q.
What can you conclude if the probabilities of P and Q are independent?
2. Watch this video of Mary's reasoning about the task:
Mary: Not wrong, just like not, like it's an "if" statement. So it's either that happens or it doesn't happen.
Andy: Oh, I see. Okay. So you're talking about this part happening or not?
Mary: Yes. So we already know that this part happens because P and Q are independent and it's asking if they're independent.
Andy: Okay.
Mary: So this is true if is a true statement in this case "if" happens. But in this one, we don't necessarily know "if" happens because this mutually exclusive is not being dependent doesn't, in my understanding of how "if" statements kind of work, being dependent has to depend on being mutually exclusive, but being mutually exclusive does not necessarily mean it's dependent. So in this case...
Andy: It sounds like each time you're looking to see if "if" is satisfied, in order to determine whether you can conclude that.
Mary: Yes.
Andy: Is that right?
Mary: Mmhmm
Andy: Is that what you're doing? Okay. Uh Let's do (c).
Solve the task below. Then, discuss with your group the following questions:
- What products would you expect your students to have after working on this task in groups?
- What would successful implementation of this task look like in your classroom? When would you implement it? (e.g. beginning, middle, end of induction unit)
- What are the challenges and affordances of using this task in your lesson?

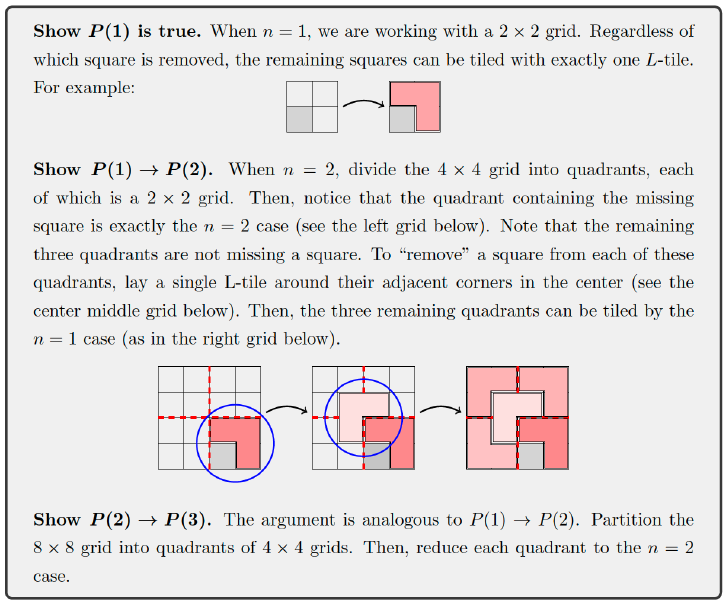
Group Discussion: What are the affordances and limitations of each of the following?
- Using an initial task that is geometric versus algebraic. e.g. L-tiles task versus the formula for the sume of the first n integers.
- Denoting the inductive implication with the variable n versus k?


- Watch the video below of Rachel's attempt to help her students bridge the gap between the outline of their quasi-inductive argument (image above) and formal induction.
- Compare what you see in the video with your own thoughts that you had written down. (e.g. bridging the gap, using n versus k, etc.)
- Share your thoughts with your group.
Rachel: Did anyone come up with a way that we could simplify rather than having to prove all of these implications? Is there a way that we could be, I guess, work smarter to just prove a simplified statement that actually demonstrates by proving that statement that every single one of these implications has been proven?
Student 1: Could you say something like P(n) implies P(n+1).
Rachel: P(n) implies P(n+1). So all of these implications, or all of the form P of one case implies P of the next case. So if I say one case is P(n), then the next case is talking about the n+1 case. So each of these I could restate as they follow the form P(n) implies P(n+1). Now we need to be a little bit careful with our use of n here. The reason why we need to be careful with our use of n is because we just said n was 500, and now we're using n as if it's variable.
Student 2: Should we just pick a different letter?
Rachel: Should we just pick a different letter? Sure. Yes.
Student 3: I would argue the only information that you can necessarily extrapolate is that you're trying to show the successor
Rachel: There you're showing the successor is true. If I wanted to rewrite this so that, think about the principle of universal generalization. When you're proving a "for all" statement, you say, introduce an arbitrary n.
Student 3: Oh yeah yeah
Rachel: I'm going to give you the argument that shows that it's true for that n. So here, I've introduced 500 as my n, and I want you to tell me how the argument's going to get me up to 500. So in that case, I'm being clear that I am still specifying a finite natural number, a specific natural number, and I'm just trying to give the argument that's going to help me climb my way up to showing that that number is true. So PJ said, could we just pick a different variable? Sure. The standard variable that you'll see is someone, we'll just call it a k. Here k is serving the role of an intermediate variable. This is our way of saying all of the intermediate cases that we need to prove in order to finally get to P(n) being true for the n that we've chosen. So these are our intermediate implications. The question is, how is this quantified? What's k? Where might, ya know, I want you to go back into your groups and I want you to figure out how you precisely quantify which k we must show this implication is true for if I want to make it all the way up to 500 being true.
At the end of the video in the previous activity, Rachel asked students to go back into their groups to "figure out how you precisely quantify which k we must show [P(k) implies P(k+1)] is true for if I want to make it all the way up to 500 being true."
Below are videos of three different groups reasoning about this task. Browse the videos and then discuss the following with your group:
- What do you notice about the students' thinking?
- What epistemological obstacles (EOs) might they be experiencing? (See table of EOs below)
- What surprises you?
Tables of Epistemological Obstacles (EOs):
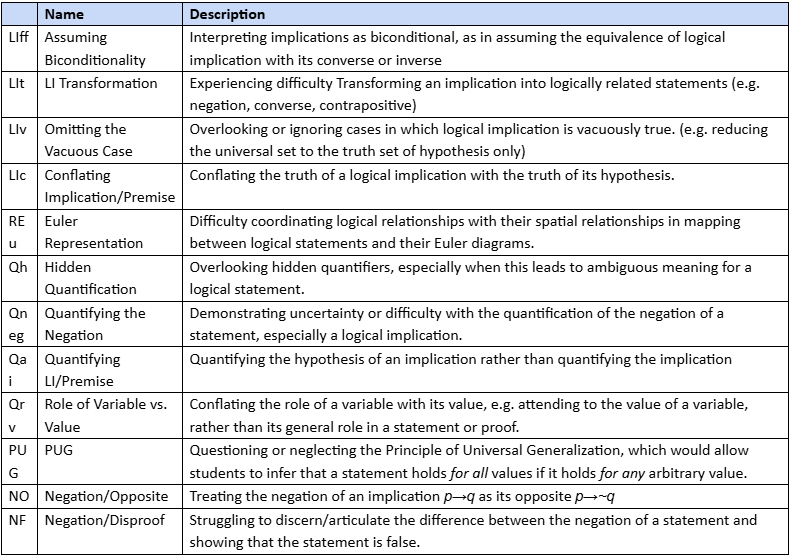
Please complete the reflection survey about your experiences today.
1. Solve the task.

2. Discuss with your group:
- For those statements that are not the negation, what might lead students to believe these are valid negations?
- Are there any other ways that you've seen students express the negation?
Group Discussion:
- What do you think are the affordances and limitations of using Euler diagrams to represent/interpret logical statements?
- Compare and contrast using truth tables versus Euler diagrams.
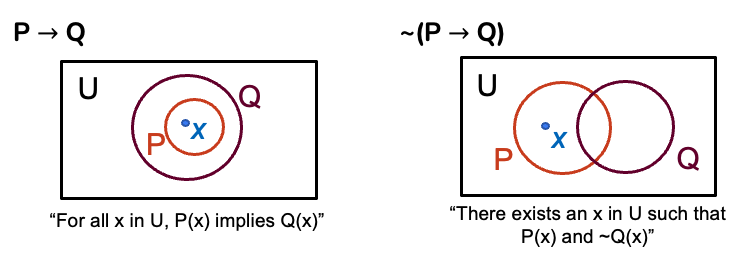
Andy and Rachel each used Euler diagrams (instead of truth tables) to support students' understanding of logical implication to their students. Watch the videos below to see how each instructor chose to introduce Euler diagrams to their students for the first time. Then discuss the following with your group:
- Compare and contrast how each instructor introduced Euler diagrams.
- How might you introduce your students to Euler diagrams?
- What concerns or hesitations do you have regarding using Euler diagrams in your classroom?
Video 1: Andy's Class
Video 2: Rachel's Class
We use this research-based instructional task to introduce students to logical implication. We adapted it from Hub & Dawkins (2018).
- Solve the task focusing on Quartet A for parts 1-4.
- With your group, make a note of the task's affordances & limitations.
Task: Below are three "quartets" of conditional statements. Read them carefully and do the following:
- Determine whether the four statements of each quartet are true or false. Use Euler diagrams to visualize the statements.
- For each implication, analyze the relationship between the set satisfying the hypothesis statement and the set satisfying the conclusion statement.
- Can you draw any conclusions about these set relationships and the truth of the implication itself?
- Compare and contrast your conclusion within each quartet. Are the statements within each quartet related to one another?
- Compare and contrast your conclusions across each quartet.

Hub, A., & Dawkins, P. C. (2018). On the construction of set-based meanings for the truth of mathematical conditionals. The Journal of Mathematical Behavior, 50, 90-102.
Explore the quartet task landing page together with you group.
Listen to student reasoning during group discussion and browse video of whole-class discussion. You don't have to watch every video. Look at a few and write down/discuss what you notice.
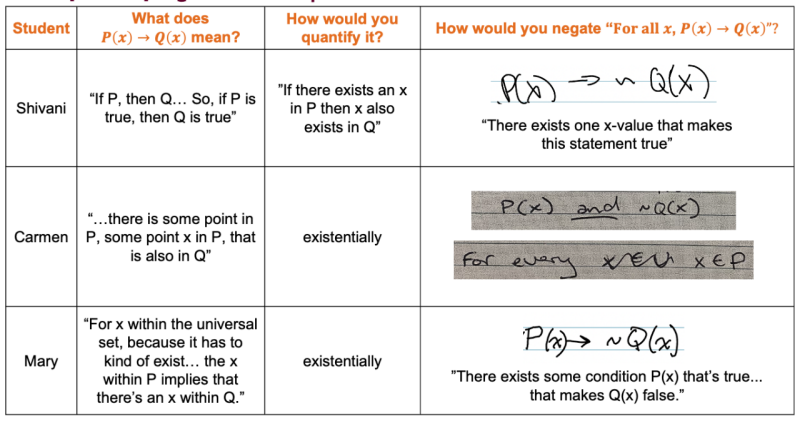
- On your own, consider the implication P(x) → Q(x). What does it mean? How might you quantify it?
- Discuss with your group.
- What challenges have you experienced during instructional interactions on quantification?
- How might you address these challenges?
Students often struggle with negating logical implications. Earlier, we saw Shivani reason about the quantification of the negation. In this activity, we'll analyze another student Carmen's thinking about the negation of the logical implication "For all x, P(x) implies Q(x)".
Below you'll find a video and transcript of Carmen's interview. After watching the video, discuss the following with your group:
- In your experience, what makes negating an implication difficult?
- How is Carmen reasoning about the difference between negating an implication and finding a counterexample?
- What else do you notice? Does anything surprise you?
Carmen : This is the part where I always mess up on. I'm not good at writing them out. So my thing is I think that with negation you're trying to find a way that the original statements, um like not necessarily the opposite, but just um like an alteration I guess to the original statement. So I don't think you're looking for a counterexample because that would just be proving that the original statement would be false. And So if negating it, you... it's still for every x and in the universe for x's in the universe or in the set. Yeah.
Andy: Um, if you're trying to prove, if you were trying to show that the original statement for all x, P(x) implies Q(x) is false, what would you do?
Carmen: P(x) implies Q(x)? So if I'm trying to show that that's false, I would just find one value in the set. Or if, are you saying x is a set for all?
Andy: So the implication I'm trying to falsify is for all x, P(x) implies Q(x). How would I show that's false?
Carmen: To show that that's false? I would just find one x where that is in P(x) but it's not in Q(x).
Andy: And that's not necessarily the same as the negation?
Carmen: I don't think so um because that's just finding a counterexample. Maybe it is. I think the negation is just kind of like doing the opposite of what it's asking for. It's not necessarily, it's not asking you to prove that something is false or to make it false, or it's like asking you to rewrite this statement that would - in a way that would make it false. Not asking you to prove that it's false, I guess. I dunno, I could be wrong, but I think...
Given that negation presents epistemological obstacles for students, how might negation best be introduced in class? In this activity, you'll explore a task Andy and Rachel have used.
- Solve the task.
- Discuss in your group: How might students respond to this task?
- Browse the videos of two student groups discussing this task. How does their thinking align with what you predicted? What surprises you?
- Check out revised task. After learning from students' responses in the videos below, Rachel re-designed and implemented a new introductory task for negation (2 years later).
Transcripts and videos can be found in the tabs below.


Please review the following links below which include an RBI Sample Unit on PMI and a sample lesson template (PDF and TeX files).
Please make sure to complete the following survey to provide feedback and choose a topic for the lesson you will create.
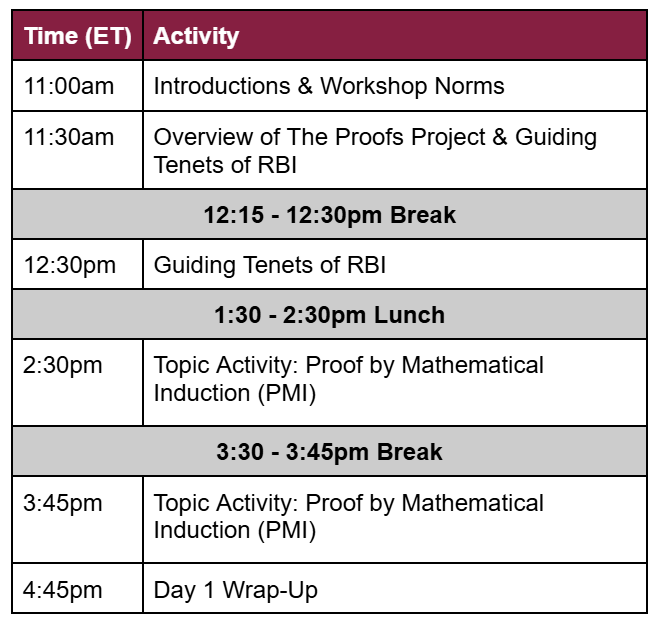
Please scroll below to see the schedule of activities followed by resources for each morning or afternoon activity.

- Meet your groups. Based on your survey responses, you've been divided into groups that indicated similar lesson topic choices.
- Determine learning objectives. What should your students know or be able to do by the end of the lesson?
- Determine norms/heuristics. What norms do you think should establish/enact to support students in meeting the learning objectives through meaningful task engagement?
- Target specific EOs. What persistent challenges do you want your students to experience and overcome?
- Collect tasks. Which tasks could you use to elicit and address EOs so that students might meet the learning objectives?
- Present. Add this information to your group's slide in the slide deck linked below. You'll have a few minutes to share your questions/concerns and ask for feedback/help from everyone.
This activity is intended to help you reflect on lesson implementation strategies before you plan the details of how you will implement your lesson's tasks in your own classroom. "The Scenarios Task," linked below, provides a demo of a research-based instructional task from start to finish. While the task is specific, our goal is for you to reflect more generally:
- Is the task the right task for meeting the outlined learning objectives?
- How is the task launched? What should be included when you launch a task?
- Predict student reasoning about this task. How do you think students will engage with it in their groups? What kinds of reasoning might we see based on whether a student holds logical implication as an action versus an object?
- Browse video of students solving the tasks and compare what you see to your predictions. How are these tasks productive for students? What reasoning might be important to address publicly in whole-class discussion? How might you connect what students are saying connect to the learning objectives for the task?
- Watch some video of the whole-class discussion. What do you notice? In what ways does the instructor solicit input from students? (e.g. what phrasing does she use to ask for contributions? How does she handle incorrect responses?, etc.) How does the instructor honor students’ reasoning & build towards formal mathematics? What norms and heuristics do you see being enacted? What does the instructor write down for students? How are EOs/learning objectives being addressed?
By now, you've selected some instructional tasks for your RBI lesson. In this activity, we outline some overarching principles that should scaffold your lesson design, and you'll think through the aspects of your tasks that make meaningful engagement possible for your students.
Guiding Principles
This section is meant as a resource for you. You can skim it now or refer to it later as needed.
The success of a task does not hinge on whether students generate correct solutions and proofs. Transition to Proof courses are playing fields where students have opportunities to connect their own initial ways of reasoning to the formal logic, language, and notation that is considered normative within the larger mathematical community. We want to help students think critically about their ideas, evaluate whether their ideas generalize, and begin to notice how subtleties of logic and language in mathematical statements impact their meaning. We consider task implementation to be successful when students have space to explore, challenge, and refine their own ways of reasoning to establish an intellectual need for making connections with normative mathematical logic. Following group work, students should be ready to talk about the key ideas -- they don't need to have solved the task.
We try not to interfere with student reasoning. Instead, we see the instructor in the role of eavesdropper -- listening in on group discussions so that they are better prepared to facilitate whole-class discussion following the task. It's important to give students ample freedom to explore their own ways of reasoning. Interjecting to push them toward more normative reasoning may reduce their intellectual need for the logical idea at hand. Sometimes, however, intervening is warranted. For example, it may be necessary to make a clarifying announcement to the class when instructors notice students have common confusions about what they have been tasked to do. We also discuss below circumstances when instructors probably should intervene to encourage equitable and inclusive group interactions.
When we ask students to share and challenge logical arguments, we need to pay careful attention to equity and inclusion during classroom interactions. For example, in inquiry-based classes, white men students often participate more frequently in discussions than women and students of color (Reinholz and Shah, 2018). In addition to assigning roles to group members to support equitable, productive collaboration on tasks, here are some simple strategies for creating a positive environment:
- Although active learning encourages students to think aloud, we shouldn't overlook the value of ``private think time.'' Many students benefit greatly from a few seconds to collect their thoughts or jot something down before group conversation. This allows students to reflect on their own thinking and share when they're ready, rather than just agreeing with what one or two more dominant, talkative students say. You might say, ``Take a minute to think to yourself about this before discussing in your groups.''
- Instructors should circulate around the room to listen in on group discussion. When one or more students are dominating the conversation, instructors should intervene to encourage plurality of contributions and ensure that other students are not being marginalized or left behind. For example, teachers might interject, ``Can you take a moment and make sure that all of your group members are on the same page?"
- Jigsaw Tasks -- tasks that require students to take responsibility for different features of the problem and rely on each other -- are even better. By designing tasks that emphasize both the responsibility of the individual and the need for collaboration, we can mitigate the potential for low- or no-participation from less dominant students. For example, if students are tasked with reading and verifying a proof, you might assign conceptual questions to each student, making it their responsibility to lead a discussion on that topic during groupwork. e.g., How is the definition of a bijection being used in this proof? How can we tell what proof technique is being used here? Probing questions you would use to generate discussion often work well for these roles. Try to create questions that "jigsaw", building off each other so that students can't just work on their on questions independently.
- Because everyone brings their own ways of reasoning to the table, instructors should help students normalize the habit of measuring progress relative to where they started rather than relative to whether they have the solution. Attend to helping each individual student move from \textsl{where they are} toward even more powerful ways of reasoning. In particular, you may take time to celebrate how the hard work students have done to overcome a particular challenge from earlier in the course is paying off in your lesson.
Discussion Questions for this Activity:
In your break-out rooms, discuss the following questions. Make note of anything that is still unresolved and what support/feedback you'd like from us for when you rejoin the main room.
- What epistemological obstacles might the task elicit/address? How might students who treat LI as an action versus object experience the task?
- What prerequisite mathematical/contextual knowledge is required? For instance, if the task uses concepts from linear algebra, you may want to plan to launch the task with a quick recap of the necessary definitions and theorems.
- What opportunities for access do students with different strengths have? Opportunities to draw a picture? If there are multiple parts, do they need to be solved in order? What opportunities are there for students to develop an object conception of LI?
- Is your task group-worthy? How can you create shared responsibility for individuals and emphasize the need to collaborate as a group? (e.g., Roles: Reporter, recorder, facilitator. See more suggestions in Guiding Principles #3)
In this activity, you'll reflect on and plan the whole-class discussions that you will facilitate within your lesson. Please use the questions below and your lesson's learning objectives to help guide you. Make a note of what aspects of your planning you'd like support/feedback on from workshop facilitators/participants.
- What student thinking is important to elicit/address publicly? Inevitably you won't have time to discuss everything. Which key ideas must be discussed? Which ideas would be nice to discuss? How might you utilize resources outside of class (e.g. homework, posting notes/extra examples, etc) to address what you didn't have time for?
- How might you do so in a way that honors students' reasoning and encourages them to share what they're actually thinking? How will you phrase your questions when you ask for student input? Rather than asking for answers/solutions, consider using more open-at ended language like:
- "What were you talking about in your groups?"
- "What was the most challenging part of this task for your group?"
- "Which part of the task were you really focused on?"
- "What ideas came up? How did your thinking change as you worked on this task?"
- What opportunities to reinforce norms and heuristics do you have while you facilitate this discussion? For example:
- Solving for the proof versus writing the proof
- Sharing what you're actually thinking rather than what you think makes you sound smart.
- Sharing ideas that are not yet fully formed and being vulnerable about gaps in understanding.
- How will you document and represent the discussion in the form of notes/boardwork? Will students write their ideas publicly? Will you? What strategies will you use to help refine students informal reasoning into precise, mathematical reasoning?
Please scroll below to see the schedule of activities followed by resources for each morning or afternoon activity.