Instructional Modules

Drawing upon past research on proof and proving, we have identified four main topics for organizing modules.
- Logical Implication
- Quantification
- Mathematical Induction
- Function
Each topic is associated with specific epistemological obstacles (EOs), which we define below. Modules specific to each topic can be accessed via the Topics tab above.
To support student learning, we suggest sociomathematical norms and heuristics for scaffolding student interactions and reasoning (see tab above). These norms and heuristics are essential for setting the stage for eliciting and addressing EOs.
Finally, we include the research-based instructional tasks that were used by Rachel Arnold in her introductory proofs class. These tasks were either pulled directly from existing literature or designed/adapted by members of The Proofs Project based on prior research.
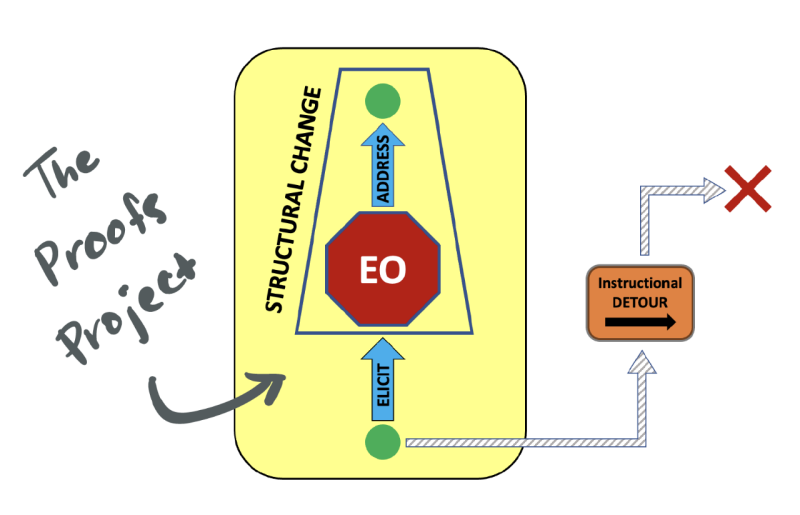
What is an epistemological obstacle (EO)?
We frame EOs as cognitive challenges that persist even in response to research-based instruction. So, EOs can be experienced both by students and teachers during instructional interactions. When instructors experience EOs, there is a tension between the desire to circumvent them and the need to provide students with opportunities to develop logical structures that are fundamental for proving. However, addressing an obstacle head on is essential for overcoming it because “it will resist being rejected and, as it must, it will try to adapt itself locally, to modify itself at the least cost, to optimize itself in a reduced field, following a well-known process of accommodation” (Brousseau, 2002, p. 85). Because EOs are persistent, students must experience an intellectual need to motivate, persevere, and successfully overcome the obstacles.
Awareness of EOs should inform the design of instructional approaches to introductory proofs topics. Traditional instructional approaches may be insufficient for addressing these obstacles, necessitating the development of alternative instructional techniques that support student learning.
Within each of the instructional modules below, we suggest ways that instructors might elicit and address epistemological obstacles (EOs) that are closely associated with each topic.
- Eliciting refers to the ways instructors might bring forth students' experiences of EOs and generate an intellectual need to address them.
- Addessing refers to ways that instructors might support students as they productively struggle through an EO, over time.
Topics
Logical implication is a conditional relation between two mathematical statements, a hypothesis and a conclusion. Reasoning through logical implication is central to proof and proving, and it is associated with many EOs.
Quantification presents additional challenges for students' logical reasoning. Quantifiers like "for all" and "there exists" make critical distinctions in the meanings of mathematical statements. Logical statements may even be multiply quantified or hiddenly quantified. This module investigates prevalent EOs associated closely with quantification.
Mathematical induction is a method of proving statements about natural numbers that poses a persistent challenge for students enrolled in proofs-based mathematics courses. Prior research indicates a number of related factors that contribute to the challenge of using this method, including EOs introduced in the Logical Implication and Quantification modules. In this module, we illustrate how those EOs manifest specifically in the context of proof by mathematical induction, and we suggest ways to address them.
Functions are centrally important objects of study in mathematics. Before taking an introductory proofs course, most students have experienced functions only as rules for computing. In proofs-based mathematics, the formal definition of functions as a relation between spaces is introduced. There is a subsequent disconnect between students' past experiences with functions as computational processes and this new, structural definition. This disconnect can lead instructors and students to experience related EOs in the classroom, especially as students are expected to consider properties of functions, their inverses, and their compositions.
Classroom norms are important tools for scaffolding effective instructional interactions. Sociomathematical norms describe normative ways for students and instructors to interact in the classroom. Unlike other classroom social norms, such as respecting one's peers and asking questions in class, sociomathematical norms are specific to mathematics. For example, we might expect our students to challenge assumptions made in proofs presented in class. The classroom norms module presents examples of norms that set the stage for eliciting and addressing EOs in introductory proofs courses. This module includes suggestions for establishing and reinforcing those norms.
Heuristics are general strategies for solving a variety of mathematical problems across contexts. An example of a commonly used heuristic is "draw a picture." Heuristics are important tools for supporting mathematical reasoning and should be integrated into introductory proof classrooms' mathematical practices. In this module, we suggest heuristics specific to proof and proving.
-
Home Item
 Alternative Language for Implications , home
Alternative Language for Implications , homeA task introducing students to alternative ways of using language to state a logical implication.
-
Home Item
 Analyzing "Proofs" of a Logical Implication , home
Analyzing "Proofs" of a Logical Implication , homeStudents are given a conditional statement and must decide whether three "proofs" do or do not prove the statement.
-
Home Item
 Determining the Validity of an Argument , home
Determining the Validity of an Argument , homeAn introductory task that supports students' understanding of what counts as a mathematically valid argument.
-
Home Item
 Proving Existence Nonconstructively , home
Proving Existence Nonconstructively , homeA task for introducing students to proving existence statements nonconstructively.
-
Home Item
 The Role of k Versus n in Mathematical Induction , home
The Role of k Versus n in Mathematical Induction , homeA task for promoting students' distinction between the role of the variable k and the variable n in proof by Mathematical Induction.
-
Home Item
 Determining How Order of Quantification Impacts Mathematical Logic , home
Determining How Order of Quantification Impacts Mathematical Logic , homeA geometric task engaging students in unpacking how the order of quantification impacts the mathematical logic of a given statement.
-
Home Item
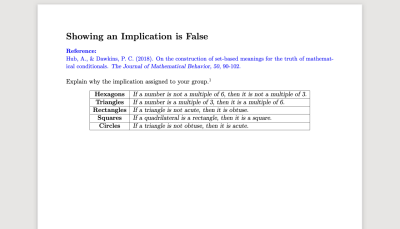 Showing an Implication is False , home
Showing an Implication is False , homeAn introductory task prompting students to think about how to show a conditional statement is false. This is a first step toward developing the precise negation of an implication.
-
Home Item
 Proving Multiply Quantified Statements , home
Proving Multiply Quantified Statements , homeA task for transitioning students from understanding how order of quantification affects mathematical logic to formally proving multiply quantified statements.
-
Home Item
 An Introduction to Multiply Quantified Statements , home
An Introduction to Multiply Quantified Statements , homeThis task gives students a first look at multiply quantified statements through five example statements.
-
Home Item
 Introduction to the Existential Quantifier , home
Introduction to the Existential Quantifier , homeThis task provides students with a first look at the existential quantifier. Students must determine when an existential statement is true and how they might prove it.
-
Home Item
 Introduction to the Universal Quantifier , home
Introduction to the Universal Quantifier , homeThis task introduces students to the universal quantifier. Students must determine when a universally quantified statement is true and how they might prove it.
-
Home Item
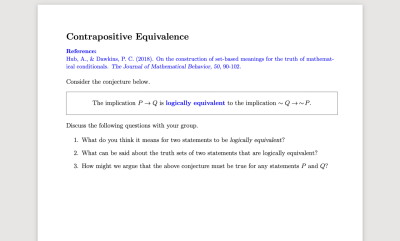 Contrapositive Equivalence , home
Contrapositive Equivalence , homeThis task supports students' understanding of why a logical implication and its contrapositive are logically equivalent.
-
Home Item
 Introducing the Concept of Negation , home
Introducing the Concept of Negation , homeThis introductory task on negation is intended to be given before stating the formal definition of negation.
-
Home Item
 Addressing Quantification of the Negation , home
Addressing Quantification of the Negation , homeThis task is intended to address students issues with quantifying the negation. It should be given after both an introductory task on and the formal definition of negation.
-
Home Item
 Properties of the Composition of Functions , home
Properties of the Composition of Functions , homeThis task is designed to support students construction of functions as objects. Given properties of the composition of two functions, they must decide whether the individual functions must inherit these same properties.
-
Home Item
 Proving Existence Constructively , home
Proving Existence Constructively , homeThis is an initial task for motivating students to recognize that a constructive existence proof should simply introduce the existent value and demonstrate that it works. This notion often runs orthogonal to students' past experience of showing the solution process for solving for an unknown in an algebraic equation.
-
Home Item
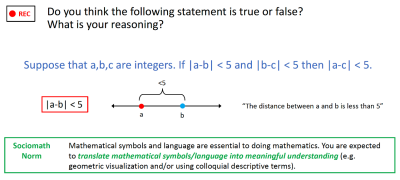 Translating Mathematical Symbols into Meaningful Understanding , home
Translating Mathematical Symbols into Meaningful Understanding , homeThis is an introductory task that can be given to students on the first day of class to begin establishing the sociomathematical norm of translating mathematical symbols and language into meaningful understanding.
-
Home Item
 Identifying Valid Mathematical Statements , home
Identifying Valid Mathematical Statements , homeThis task is a first introduction to (open) mathematical statements. Students are given an open expression and an open statement and must discuss whether they are mathematical statements. It encourages students to notice the importance of quantifying variables.
-
Home Item
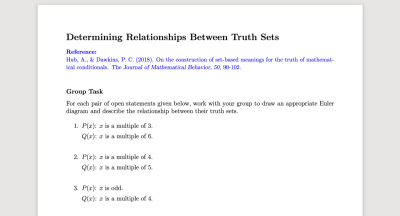 Determining Relationships Between Truth Sets , home
Determining Relationships Between Truth Sets , homeIn this tasks, students are given pairs of open statements and asked to determine the relationship between their truth sets via generating their own Euler diagrams. This can be used as a first task after students have been given the definition of the truth set of an open statement and been introduced to visualizing truth sets via Euler diagrams.
-
Home Item
 Logical Implication: The Quartets Task , home
Logical Implication: The Quartets Task , homeThis introductory task should be used immediately following statement of the definition of a logical implication (or conditional statement). Students are given quartets of conditional statements to compare and contrast. This supports students to develop an understanding of logical implication based on truth sets represented through Euler diagrams. Students are invited to notice and abstract common logical structure across all three quartets.
-
Home Item
 Using Euler Diagrams to Understand a Vacuously True Implication , home
Using Euler Diagrams to Understand a Vacuously True Implication , homeThis task engages students with the truth of an implication with a false hypothesis.
-
Home Item
 Visualizing an Implication with a False Hypothesis , home
Visualizing an Implication with a False Hypothesis , homeThis task supports students' understanding of a vacuously true implication through the use of an Euler diagram. Pairs well as a follow-up to "Using Euler Diagrams to Understand a Vacuously True Implication".
-
Home Item
 Understanding the Negation of an Implication , home
Understanding the Negation of an Implication , homeThis task supports students' understanding of the relationship between the truth set of an implication and its negation.
-
Home Item
 Reinventing the Principle of Mathematical Induction , home
Reinventing the Principle of Mathematical Induction , homeThese tasks comprise an entire instructional unit on the principle of mathematical induction, where students reinvent the necessary logical components of proof by induction and reason about the necessity of the base case, the logic of the inductive implication, as well as determining the appropriate quantification.
-
Home Item
 The Principle of Mathematical Induction: Scenarios , home
The Principle of Mathematical Induction: Scenarios , homeThis task supports students' abstraction of the underlying logic for quasi-inductive arguments so that they might conjecture the formal Principle of Mathematical Induction. Students have opportunities to play with various logical components to determine whether they combine to to prove that a statement must be true for all natural numbers.


