Logical Implication

"Implication is at the very heart of mathematical reasoning."
--Viviane Durand-Guerrier (2003)
As you will see in this instructional module, logical implication poses consistent challenges for students. Due to its central importance within logical reasoning, students must be given opportunities to experience and address these challenges head-on.
We frame student reasoning about logical implications, or conditional statements, using an action-object perspective (Piaget, 1970; Dubinsky, 1991). As an action, a logical implication involves three components: a predicate, P; a conclusion, Q; and a transformation between them.
Students who treat implications as actions can reason by modus ponens:
- If P, then Q.
- P is true.
- Therefore, Q is also true.
However, in treating implications as actions across three components, rather than as single objects, students might experience persistent challenges in transforming and quantifying them. In particular, they might not reason by modus tollens:
- If P, then Q.
- Q is false.
- Therefore, P is also false.
Identified Epistemological Obstacles
This module focuses on the following epistemological obstacles that students can and should experience when learning how to reason with logical implication.
As discussed above, students may treat logical implications as actions or as objects. When treating the implication "P implies Q" as an action, a student might use the truth value of P to determine the truth value of Q. Rather, when treating this implication as an object, a student can take the implication as an invariant relationship which they might transform (say into its converse or contrapositive) or quantify.
Tasks like the one shown below can be used to elicit the ways that students treat (and prove) logical implications.
Notice that the task above involves proving a logical implication that is universally quantified ("for all x"). The video below shows the instructor introducing this task to her students. Following this introduction, students then began working in their groups, at their respective tables.
The video shown below illustrates how the students at one table (the Triangle Group) engaged with this instructional task. In particular, the students in this group disagree about the validity of Proof 1.
The task elicited a lot of discussion among the students:
- In proving a universally quantified implication, is it enough to begin with an arbitrary value as Proof 1 did?
- What exactly does Proof 2 prove, if anything?
- And, is Proof 3 a proof of the negation or contrapositive of the original implication?
Following group discussion, the teacher solicited responses from students across the class (see the two videos below). Most students agreed on the validity of Proof 1, but there was less agreement about Proof 3. This may be because Proof 1 involves a direct application of modus ponens--taking the truth of hypothesis as given and then demonstrating the truth of the conclusion (Q) follows--which is accessible to students who treat logical implications as actions. In contrast, Proof 3 involves a transformation of the original implication into its contrapositive.
This video shows class discussion of which proofs are valid and, in particular, why Proof 1 is valid.
In this next video, the class discusses why or why not they believe Proof 3 (a proof by contrapositive) is valid. Students' are prompted to analyze the logical structure of the proof. Because part of the argument is proven by contradiction, the instructor discusses why proof by contradiction may be used to establish that a statement is true.
The teacher began addressing the ways students treat logical implications, including the language they use to describe them, with tasks like the one shown below.
In working on this task, students considered various ways that the same logical implication might be expressed, including expressions of the contrapositive. The video below shows students' productive struggles (within the Circle group) in determining which statements provided different expressions of the same mathematical object--the original logical implication.
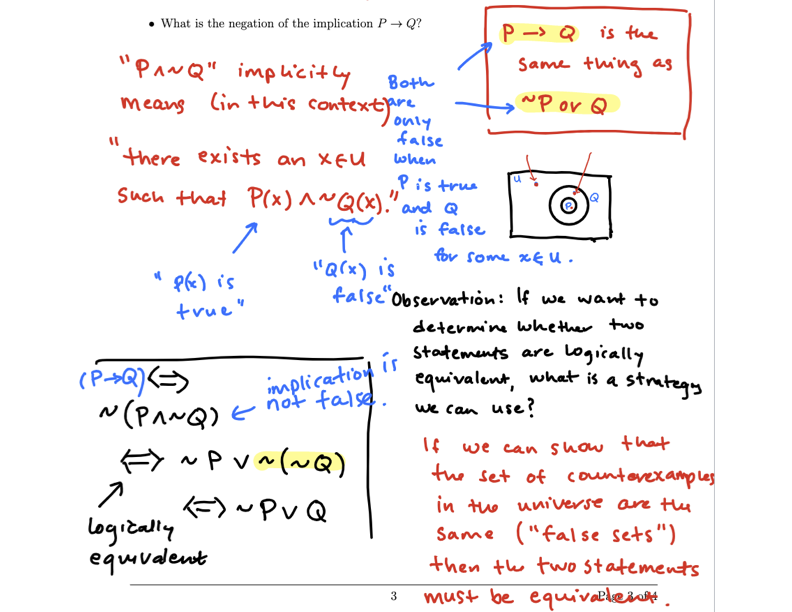
Related to the prior obstacle, students often struggle to transform logical implications into their negations, converses, and contrapositives. Teachers can elicit such challenges simply by asking students to state the negation of an implication; i.e., what statement would need to be true in order for the implication to be false?
In the video shown below, the instructor points to the equivalence shown in the upper-right corner of the image above and asks students how they know the two statements ("P implies Q" and "~P or Q") are indeed equivalent.
One student in the class offered that two statements are equivalent if they have the same "false set," or set of counterexamples.
The instructor built on this idea by asking students to work in groups on the task shown below. This task requires students to consider the logical equivalence of an implication and its contrapositive and to generalize the idea of logical equivalence.
Reponses for the Triangle group are included below. Note that the students explained equivalence in terms of truth sets and then used Euler diagrams to represent relationships between these sets.
And the video shown below includes discussion from the Circle group as they work through the same task. They also discuss truth sets (and false sets) but represent them with a truth table.
To help students address challenges associated with transforming logical implications, the instructor assigned two homework problems that involved analyzing whether two statements were logically equivalent and converting statements into their contrapositives and negations (see image below).
In the video shown below, the Square group shares their responses to the homework problems. Notice that, in discussing Problem 1, two of the students began discussing the role of the vacuous case in determining the negation of an implication.
When reasoning with logical implications, students sometimes assume bidriectionality (biconditionality)--that P implies Q also means that Q implies P. This assumption might be a product of pragmatic interpretations of everyday language. For example, when we say "if you eat your dinner, then you can have dessert," we actually take this to mean that "you can have dessert if and only if you eat your dinner."
In the following video, when the instructor asks her class why we might call "If P, then Q" a conditional statement, one student suggests "because Q only happens if P happens." The instructor uses this opportunity to elicit students' experience of the epistemological obstacle (assuming biconditionality), and asks, "Is there any circumstance in which Q could still be true, even when P is not?"
To address this epistemological obstacle, the instructor asks the students to work in their groups on the task below. This task leverages drawing Euler diagrams for the conditional statement, "if P, then Q" to promote students' logical distinction between an implication and its converse.
The next video shows the instructor launching the task.
The following video shows responses from the Hexagon group. Notice there is some initial confusion about whether Q should be drawn within P, or whether P should be drawn within Q. One of the students uses the latter relationship to argue for the equivalence of the contrapositive, ~Q implies ~P.
And, the next video comes from the Triangle group. After drawing the same Euler diagram, these students argue that "you can only have P if you also have Q." Later in the video, students discuss whether "P can be a subset of Q and Q be a subset of P."
As exemplified in prior videos, students may leverage Euler diagrams to reason through the logic of conditional statements . Because Euler diagrams depict implications via a subset relationship, they may encourage students to abstract the invariant relationship between the hypothesis and the conclusion. That is, they might encourage students to begin development of an object conception of logical implication.
However, students' interpretations of Euler diagrams can be problematic, especially with regard to quantification. For example, when visualizing "P implies Q" as the truth set of P drawn within the truth set of Q, students might further infer that there exist elements in the set Q that are not in P. This, however, is not true for the biconditional case when P and Q have the same truth set. In this case, the space outside of P and inside of Q is empty.
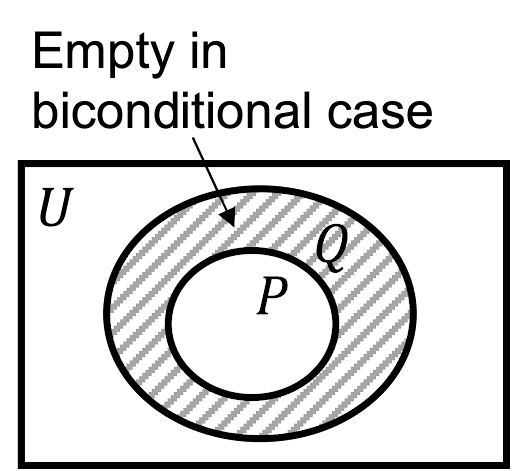
Similarly, Euler diagrams may hide the vacuous case.

Moreover, even when a nonempty, closed region does correspond to a nonempty truth set, it does not indicate how many elements of the universe lie in this region. Opportunities to experience these ambiguities must be elicited and addressed.
To elicit some of the challenges related to interpreting logical implications with Euler diagrams, the instructor raised the following "fundamental questions" to the class.
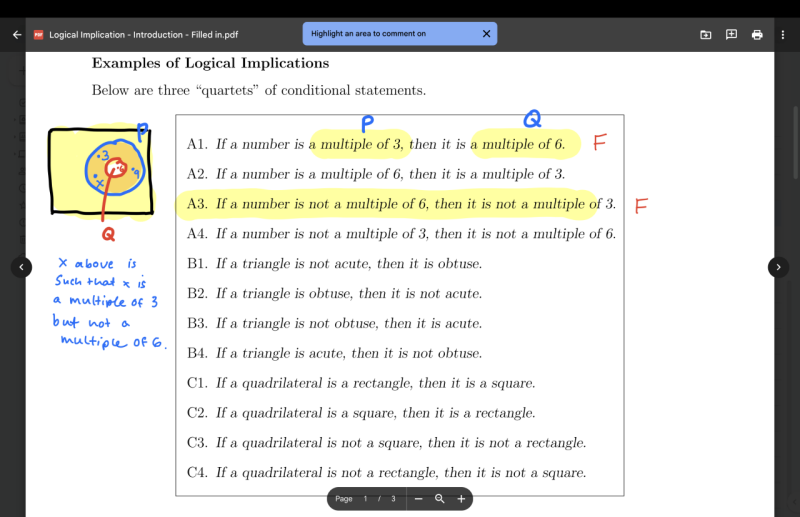
Following the introduction of those questions, the instructor asked students to work within their groups to evaluate the validity of the "quartets" of statements shown below.
The Rectangle group worked through the first quartet, using an Euler diagram to justify their evaluations. Notice that the students realize they can use the same diagram to consider each statement in the quartet.
Following discussion about the prior group work on the quartets, the instructor noted that some students used Euler diagrams to establish a logical equivalence between the general implication, P implies Q, and its contrapositive, ~Q implies ~P. So, she asked students to return to their groups to explore, and possibly justify, this relationship.
The following two videos show how the instructor framed the issue and illustrate responses from two different tables: the Circle group and the Rectangle group.
Notice that the students in the Circle group express some uncertainty about the relation between the truth set of P and the truth set of Q, as represented by an Euler diagram. Consequently, they question the logical equivalence of the implication and its contrapositive. Students in the Rectangle group express similar uncertainties about the logical relationships.
What Research Says...
Prior literature has identified multiple challenges related to student reasoning with logical implications. For example, students tend to interpret a conditional statement (if P, then Q) as a biconditional one (P if and only if Q) (e.g., Girotto, 1990; Wilkins, 1928). Although such interpretations are not valid from the standpoint of formal logic, they are deeply rooted in everyday language and can be explained from a pragmatic point of view (Epp, 1999; Geis & Zwicky, 1971; Rumain et al., 1983; Wagner-Egger, 2007). Transforming logical implications presents a related challenge. Empirical studies have shown that undergraduate students often conflate an implication with its converse (Durand-Guerrier, 2003; O’Brien et al., 1971) and with its inverse (Goetting, 1995; Knuth, 1999, 2002). Other scholars reported on students’ struggles to understand the equivalence between an implication and its contrapositive (Dawkins & Hub, 2017; Stylianides et al., 2004) or between an implication and a disjunction (Hawthorne & Rasmussen, 2015).