Slimane Adjerid

460 McBryde Hall, Virginia Tech
225 Stanger Street
Blacksburg, VA 24061-1026
Many physical phenomena are represented by systems of partial differential equations having solutions with local and nonuniform multi-scale behavior such as moving fronts and boundary layers observed in fluid and solid dynamics, and material interfaces. Since these nonuniformities and singularities may form, evolve, and disappear with time, standard numerical methods become either very inefficient or impossible to use. However, Adaptive methods with variable mesh sizes and orders of approximation and non standard finite element spaces and formulations in both time and space are very efficient in resolving local nonuniform behaviors.
FULLY ADAPTIVE METHODS: Efficient and robust algorithms use information available during the computations to improve the quality of the solution and are guided by error estimates which indicate that elemental discretization error decrease by either decreasing the element size h or h-refinement, by increasing the polynomial degree p or p-refinement, or by repositioning the finite element vertices to equilibrate the mesh. Our software combines these enrichment techniques to obtain optimal algorithms for various time dependent systems.
ERROR ESTIMATION: In the heart of fully adaptive algorithms lie some error estimators or indicators. Usually, error estimators or indicators are obtained by solving local problems using an approximation of degree higher that the finite element solution. We continue to work in this area and develop more efficient and reliable error estimators that can be used to control the accuracy of the solution.
DISCONTINUOUS GALERKIN METHODS: Discontinuous Galerkin methods are a relatively new class of finite element methods for partial differential equations. We investigate the superconvergence behavior and construct efficient errors estimators which are used to guide adaptive algorithms and search for new formulations.
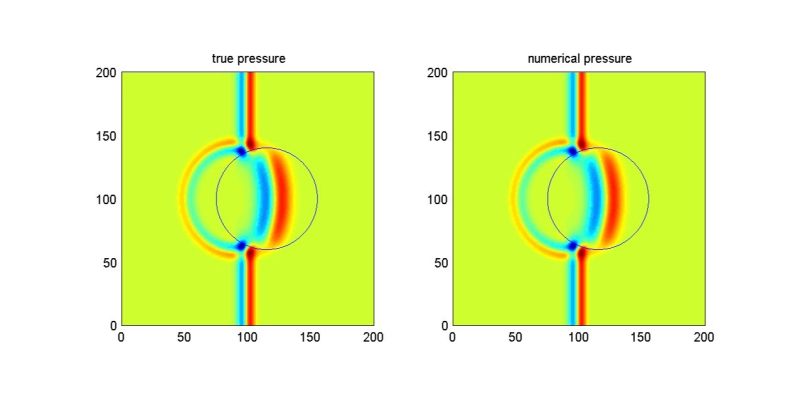
IMMERSED FINITE ELEMENT METHODS: A popular technique that adapts both the finite element formulation and spaces to construct highly accurate solutions for interface problems modeled by partial differential equations with discontinuous coefficients or completely different systems of partial differential equations. We propose several immersed finite element methods that allow elements to be cut by the interface and, thus, they contain more than one material. The proposed piecewise polynomial spaces partially or fully solve the problem on interface elements. Applications include, but not limited to, the standard diffusion interface problems, flow interface problems and acoustic elastic wave propagation in inhomogeneous media.